Summary
Data security is crucial in today’s interconnected digital landscape, where data must be securely stored in the cloud and transmitted globally for its intended purpose. It is essential to safeguard data from unauthorized access, both during storage and while transferring it over potentially insecure infrastructure. Whether you’re a developer, DevOps professional, or a security engineer, it is critical to apply the correct cryptographic algorithms when securing data at rest or during transit. This marks the first article in our series, ‘Securing Data at Rest and During Transit: Exploring Cryptographic Algorithms and Primitives’.
In this article, we will delve into explaining the purpose of cryptographic algorithms and gain an understanding of the various cryptographic primitives and algorithms used to ensure confidentiality, integrity, and authenticity.
Target audience
This article provides valuable insights for developers, DevOps professionals, test engineers, and security engineers who are tasked with applying and reviewing cryptographic algorithms for data security, whether at rest or during transit. It’s also a great resource for anyone looking to understand cryptographic algorithms and determine which ones to use in specific cases to achieve their security goals.
Cryptographic primitives and algorithms
Cryptographic Primitives
Cryptographic primitives are fundamental building blocks of cryptographic systems. A primitive is the smallest useful construction in cryptography, which is often used with other primitives in order to build a protocol. They are basic mathematical operations or algorithms that serve as the foundation for constructing more complex cryptographic schemes. Examples of cryptographic primitives include hash functions, encryption algorithms, digital signature algorithms, random number generators, substitution-permutation networks, block ciphers, stream ciphers and key expansion.
Cryptographic Algorithms
Cryptographic algorithms are specific implementations or protocols that use one or more cryptographic primitives to achieve a particular security goal. These algorithms outline the step-by-step procedures for performing operations like encryption, decryption, digital signing, and hashing. Examples of cryptographic algorithms include Rivest-Shamir-Adleman (RSA), Advanced Encryption Standard (AES), Elliptic Curve Digital Signature Algorithm (ECDSA), (Elliptic Curve Diffie-Hellman Ephemeral (ECDHE) and SHA-2 family Secure Hash Algorithm with 256 bits (SHA-256).
Key Difference
The key difference between cryptographic primitives and cryptographic algorithms lies in their level of abstraction. Cryptographic primitives are low-level mathematical operations that are used as building blocks to construct higher-level algorithms. Cryptographic algorithms, on the other hand, are complete protocols or procedures that leverage these primitives to achieve specific security objectives.
Cryptographic algorithms utilize cryptographic primitives to achieve their security goals. For instance, an encryption algorithm like AES employs primitives like substitution-permutation networks, block cipher, and key expansion to secure data. Cryptographic primitives can be combined and configured in various ways to create different algorithms that address different security requirements.
Purpose of Cryptographic Algorithms
Cryptographic algorithms are used to provide Confidentiality, Data Integrity, and Authentication.
Confidentiality
Confidentiality is achieved by encrypting the data when it is stored in any location in the cloud or transferred across the internet. Cryptographic algorithms ensure that data is encrypted by the sender and can only be decrypted by its intended recipient. This security is maintained through a secret key possessed by both the sender and receiver.
Types of Cryptographic Algorithms
There are primarily two types of cryptographic algorithms used for encryption and decryption: Symmetric Key Encryption and Asymmetric Key Encryption. Symmetric Key encryption is also called secret key cryptography, while Asymmetric Key encryption is known as public key cryptography.
Symmetric Key Encryption
Symmetric key encryption employs a single, shared key for both encryption and decryption, making it faster and more efficient than asymmetric encryption. It’s highly suitable for bulk data encryption due to its speed and simplicity. However, the challenge lies in securely exchanging the secret key between parties, as any compromise of this key can compromise the security of the entire communication. Various key exchange methods and secure key management practices are essential to mitigate this risk. Symmetric encryption is widely used for securing large data sets and real-time communications where performance is critical.
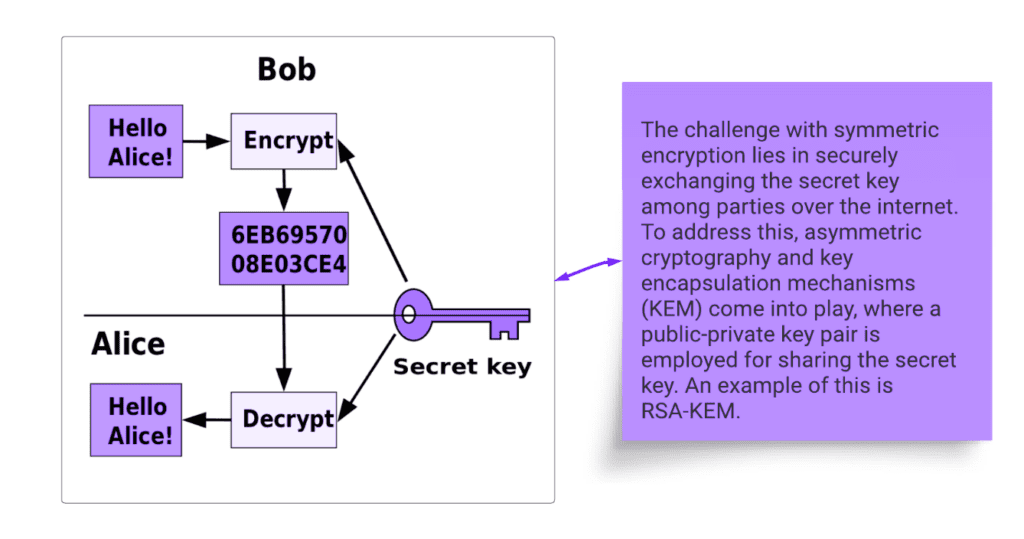
Some common examples of symmetric encryption algorithms include AES, Digital Signature Algorithm (DSA), and 3DSA. Among these, AES stands out as the most widely used encryption algorithm, while DSA and 3DSA are considered outdated and are not recommended.
Advanced Encryption Standard (AES)
AES is a widely used symmetric encryption algorithm that provides a high level of security. It operates on fixed-size data blocks and supports key lengths of 128, 192, and 256 bits. AES ensures data confidentiality by transforming plaintext into ciphertext using a secret encryption key. The same key is employed for both encryption and decryption, underscoring the importance of safeguarding the key.
Asymmetric Encryption
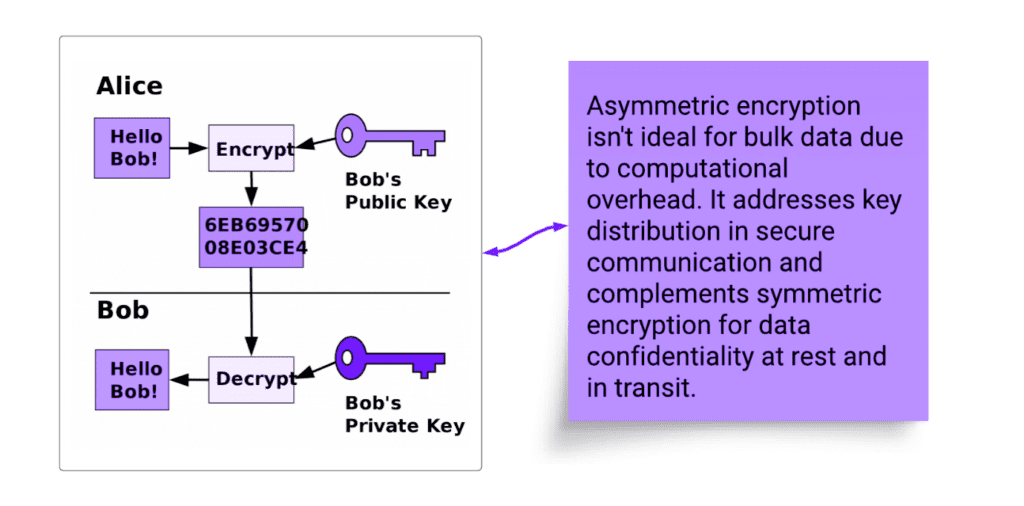
Asymmetric key encryption, or public-key encryption, uses a pair of keys – public for encryption and private for decryption. While slower than symmetric encryption, it excels in secure key exchange, where parties can securely communicate without sharing a common secret key. It complements symmetric encryption by exchanging secret keys securely, addressing its primary challenge. However, it’s less efficient for bulk data encryption due to its performance. Examples of asymmetric algorithms include RSA, Elliptic Curve Cryptography (ECC), Diffie-Hellman, and Digital Signature Algorithm (DSA), each offering different levels of security and efficiency for various use cases.
Key Exchange
Key exchange algorithms serve the primary purpose of securely sharing cryptographic keys between parties involved in secure communications. They address the problem of ensuring that both the sender and receiver possess a shared secret key for encrypting and decrypting data, even when they communicate over potentially insecure channels. By securely exchanging keys, key exchange algorithms establish a foundation for data confidentiality and secure communication. Diffie-Hellman (DH), Diffie-Hellman Ephemeral (DHE), RSA, and ECDHE are examples of key exchange algorithms.
Diffie-Hellman & Diffie-Hellman Ephemeral (DH & DHE)
Diffie-Hellman allows two parties to jointly derive a shared secret key over an insecure communication channel. It’s widely used and forms the basis for many secure communication protocols. However, DH doesn’t provide authentication on its own. In DH, the source parameters used to generate private and public keys are static, so it does not offer Perfect Forward Secrecy (PFS). In another form of DH called Diffie-Hellman Ephemeral (DHE), the source parameters are ephemeral and provide PFS. Hence, DHE is recommended over DH.
Rivest-Shamir-Adleman (RSA)
RSA is a popular asymmetric encryption algorithm that uses a pair of keys: a public key for encryption and a private key for decryption. It’s widely used for securely exchanging symmetric encryption keys. While not as efficient as symmetric encryption for encrypting large amounts of data, RSA provides a mechanism for securely sharing confidential information. Additionally, RSA does not provide perfect forward secrecy (PFS). This means that if an attacker obtains the private key, they can decrypt past communications. To address these challenges, some opt for alternatives like Diffie-Hellman variants (e.g., DHE or ECDHE), which offer better performance and PFS.
Elliptic Curve Diffie-Hellman Ephemeral (ECDHE)
ECDHE uses elliptic curve cryptography to achieve the same purpose as Diffie-Hellman but with smaller key sizes, making it more efficient.
Data Integrity
While encryption ensures that data remains confidential, it does not prevent malicious alterations. If data is tampered with during storage or transmission, it could compromise the accuracy and trustworthiness of that data. Hence along with confidentiality, it is equally crucial to maintain the integrity of data during storage or transmission. Here’s why data integrity is essential and how it complements confidentiality.
- Verification of Data Authenticity
Data integrity measures, like hashing or Message Authentication Codes (MACs), enable the recipient to verify that the data they receive is authentic and unaltered. This is especially important in scenarios where data needs to be accurate and trustworthy, such as financial transactions, legal documents, or critical system files.
- Detection of Tampering
Data integrity mechanisms can detect any accidental or intentional changes to the data, even if they are minor. By comparing the hash value or MAC of the received data with the expected value, any variances can be identified, alerting you to potential tampering or corruption.
- Data Trustworthiness
In contexts like healthcare, legal, or financial sectors, the trustworthiness of data is paramount. Maintaining data integrity ensures that records, transactions, and sensitive information can be relied upon with confidence. This trust is built on the assurance that the data has not been tampered with.
In summary, confidentiality alone, while crucial for protecting data from prying eyes, cannot guarantee the accuracy and trustworthiness of that data. Data integrity, through cryptographic algorithms, provides the means to verify that the data has not been altered, intentionally or unintentionally, during storage or transmission. This dual approach of confidentiality and data integrity is fundamental for securing sensitive information in various domains, ensuring its secrecy and reliability. Cryptographic algorithms for data integrity, such as hash functions, Message Authentication Codes (MAC) and, message digest, provide a means to detect any unauthorized changes.
Hash Functions
SHA-2 family Secure Hash Algorithm with 256 bit (SHA-256): SHA-256 is a cryptographic hash function that produces a fixed-size hash value (256 bits) from any input data. It’s widely used for verifying data integrity. Even a slight change in the input data results in a significantly different hash value. By comparing the computed hash of received data with the original hash, one can determine if the data has been tampered. MD5, SHA-1, SHA-2 family (SHA-224, SHA-256, SHA-384, SHA-512/224 and SHA-512/256), and SHA-3 family (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) are examples of hash functions. However, MD5 and SHA-1 are deprecated and no longer recommended due to vulnerabilities and potential exploits.
Message Authentication Codes (MACs)
A Message Authentication Code (MAC) is a short piece of data that’s derived from the content of a message and a secret key. It’s used to verify the integrity and authenticity of a message. Unlike digital signatures, MACs are often symmetric, meaning the same key is used for both generating and verifying the MAC. The sender creates the MAC using their secret key and attaches it to the message. The recipient, who also knows the secret key, can then generate the MAC from the received message and compare it with the received MAC to ensure that the message has not been tampered with. MACs provide integrity and authentication, but they don’t provide non-repudiation because both parties share the same secret key, and either party could generate a valid MAC. Keyed-Hash MAC (HMAC), KECCAK, MAC (KMAC) and CMAC are examples of MACs.
Authentication
Authentication is the process of verifying the identity of parties in a communication. While confidentiality and integrity protect data from unauthorized access and tampering, they don’t guarantee the source’s authenticity. Authentication ensures the sender’s legitimacy, preventing malicious impersonation. It solves the key problem of establishing trust between parties in data transmission. Digital signatures, a common method for authentication, use asymmetric encryption. The sender encrypts a message with their private key, and the recipient decrypts it with the sender’s public key. If decryption succeeds, it confirms the sender’s identity and the data’s integrity, providing a secure means of authentication.
Digital Signatures
A digital signature is like a virtual fingerprint that is unique to the sender and the content of a message. When you digitally sign a message, you use your private key to create a signature. This signature is attached to the message, and anyone with access to your public key can verify that the signature matches the message and that it was indeed generated by you. Digital signatures provide non-repudiation by ensuring that the sender can’t deny sending the message because their signature serves as undeniable proof of their involvement.
Algorithm Steps
- Key Generation: A user generates a pair of cryptographic keys – a private key and a corresponding public key e.g., using an elliptic curve.
- Signing: To sign a message, the sender applies a mathematical function to the message and their private key to produce a digital signature. This signature is sent along with the message.
- Verification: The recipient can then use the sender’s public key to verify the authenticity of the message. The signature and the original message are processed using the public key and a verification process. If the signature is valid, the message is considered authentic.
Difference between Signing and Encrypting
- Signing is not similar to encrypting the message. Both uses asymmetric algorithm with public/private key pair, but the purpose is different. Signing is to achieve authenticity and integrity while encryption’s primary purpose is to achieve confidentiality. For example, consider a legal contract that needs to be electronically signed. When a person digitally signs the contract, it creates a unique digital signature that is based on the content of the contract and the signer’s private key. This signature is then attached to the contract. If there is a dispute later, the signature can be verified to prove that the person signed the contract and that the contract content has not been altered.
- In case of encryption consider an example of online banking. When you log in to your bank’s website, the communication between your computer and the bank’s server is often encrypted. This ensures that even if an attacker intercepts the data being transmitted, they cannot decipher the sensitive information (like your username and password) without the encryption key. However, encryption alone does not prove that you are indeed the account holder; it only secures the data in transit.
Digital signature algorithms
Rivest-Shamir-Adleman (RSA)
RSA is a widely used Digital Signature Algorithm, ensuring data integrity and authenticity. It employs a public-private key pair for signing and verifying messages. However, RSA faces challenges in scaling and performance, particularly for large-scale, resource-intensive operations, which can slow down cryptographic processes. This prompts the need to explore alternatives like Elliptic Curve Digital Signature Algorithm (ECDSA), which offers robust security with faster execution, making it more suitable for modern, high-performance systems and applications.
Digital Signature Algorithm (DSA)
DSA is another widely used algorithm for creating digital signatures. It provides a way to ensure non-repudiation, meaning the signer cannot later deny signing the message. DSA uses mathematical properties related to discrete logarithms to create and verify signatures.
Elliptic Curve Digital Signature Algorithm (ECDSA)
ECDSA is a widely used digital signature algorithm that provides a way to verify the authenticity of digital messages or documents. It is based on the mathematical properties of elliptic curves and is particularly well-suited for resource-constrained environments such as mobile devices due to its smaller key sizes compared to other traditional algorithms.
Comparisons between RSA, DSA and ECDSA
Performance:
- ECDSA is generally more efficient in terms of computation and storage compared to RSA and DSA. This is due to the smaller key sizes required while still maintaining strong security. Smaller key sizes mean faster computations and less memory consumption.
- RSA is based on the mathematical difficulty of factoring large composite numbers into their prime factors. It has been widely used for digital signatures and encryption. However, RSA key lengths need to be significantly larger than those of ECDSA to achieve the same level of security. This leads to slower performance, especially in resource-limited environments.
Security:
The security of ECDSA depends on the hardness of the elliptic curve discrete logarithm problem. ECDSA offers a level of security equivalent to the key length used. For example, a 256-bit ECDSA key provides similar security to a 3072-bit RSA key. This means that ECDSA can offer strong security with shorter key lengths, making it a good choice for environments where resource constraints are a concern.
- DSA is based on the discrete logarithm problem in a finite field. It’s commonly used for digital signatures. Like RSA, DSA requires larger key sizes compared to ECDSA to achieve similar security levels.
About the Author
Kashyap Joshi serves as AVP of Software Engineering at Zimetrics Technologies, and brings extensive experience in software development, operations, and engineering across diverse domains, spanning desktop to cloud applications. He is dedicated to engineering excellence and actively champions best practices in software engineering, data security, and cloud security.
References
- Serious Cryptography: A Practical Introduction to Modern Encryption Paperback – 6 November 2017 by Jean-Philippe Aumasson https://amzn.eu/d/hIVYAqV
- Real-World Cryptography Paperback – Import, 12 October 2021 by David Wong https://amzn.eu/d/ggcTa49
- NIST recommendations for Message Authentication Code https://csrc.nist.gov/Projects/Message-Authentication-Codes
